Chapter 12. 균형 잡힌 이진 탐색 트리 : AVL 트리의 구현
주의 사항!
- 이 글은 제가 직접 공부하는 중에 작성되고 있습니다.
- 따라서 제가 이해하는 그대로의 내용이 포함됩니다.
- 따라서 이 글은 사실과는 다른 내용이 포함될 수 있습니다.
AVL 트리의 경우는 이론적인 이해만으로도 의미가 있기 때문에 시간이 부족하거나 더 이상의 코드 분석이 부담스럽다면 AVL트리의 이론적인 이해에 만족하고 다음 Chapter로 넘어가도 좋다고 합니다. 하지만 저는 AVL 트리를 구현하는 것까지 마무리해 보고자 합니다.
AVL 트리도 이진 탐색 트리이므로, 앞서 구현했던 이진 탐색 트리의 파일들을 확장하여 AVL 트리를 구현하고자 합니다. 그리고 다음의 두 파일을 추가하여, 리밸런싱을 진행하는데 필요한 도구들을 선언하고 정의하겠습니다.
- AVLRebalance.h 리밸런싱 관련 함수들의 선언
- AVLRebalance.c 리밸런싱 관련 함수들의 정의
그리고 이진 탐색 트리의 파일들을 확장하기에 앞서 해당 파일들이 어떻게 구성되어 있는지 먼저 보이겠습니다.
//BinaryTree.h 헤더 파일로 저장
//수정 날짜 : 2021.03.23
//작성자 : KOEY
#ifndef BINARYTREE_H
#define BINARYTREE_H
typedef int BTData;
typedef struct BTreeNode
{
BTData data;
struct BTreeNode* left;
struct BTreeNode* right;
} BTreeNode;
typedef void(*Action)(BTreeNode*);
BTreeNode* MakeBTreeNode(void); //노드를 생성 및 초기화하고 그 주소 반환
BTData GetData(BTreeNode* bt); //노드의 데이터 반환
void SetData(BTreeNode* bt, BTData data); //노드에 데이터 저장
BTreeNode* GetLeftSubTree(BTreeNode* bt); //왼쪽 자식 노드의 주소 반환
BTreeNode* GetRightSubTree(BTreeNode* bt); //오른쪽 자식 노드의 주소 반환
void MakeLeftSubTree(BTreeNode* main, BTreeNode* sub); //왼쪽 자식 노드에 서브 트리 삽입
void MakeRightSubTree(BTreeNode* main, BTreeNode* sub); //오른쪽 자식 노드에 서브 트리 삽입
void ChangeLeftSubTree(BTreeNode* main, BTreeNode* sub); //왼쪽 자식 노드 변경, main에 부모 노드, sub에 자식 노드 주소 전달
void ChangeRightSubTree(BTreeNode* main, BTreeNode* sub); //오른쪽 자식 노드 변경, main에 부모 노드, sub에 자식 노드 주소 전달
void DeleteTree(BTreeNode* bt); //해당 노드를 루트 노드로 가지는 트리 삭제
void PreorderTraversal(BTreeNode* bt, Action act); //전위 순회
void InorderTraversal(BTreeNode* bt, Action act); //중위 순회
void PostorderTraversal(BTreeNode* bt, Action act); //후위 순회
#endif//BinaryTree.c 소스 파일로 저장
//수정 날짜 : 2020.03.23
//작성자 : KOEY
#include "BinaryTree.h"
#include <stdlib.h>
#include <stdio.h>
BTreeNode* MakeBTreeNode(void)
{
BTreeNode* newNode = (BTreeNode*)malloc(sizeof(BTreeNode));
if (newNode == NULL)
{
printf("메모리 공간이 부족합니다.\n");
exit(1);
}
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
BTData GetData(BTreeNode* bt)
{
return bt->data;
}
void SetData(BTreeNode* bt, BTData data)
{
bt->data = data;
}
BTreeNode* GetLeftSubTree(BTreeNode* bt)
{
return bt->left;
}
BTreeNode* GetRightSubTree(BTreeNode* bt)
{
return bt->right;
}
void MakeLeftSubTree(BTreeNode* main, BTreeNode* sub)
{
DeleteTree(main->left);
main->left = sub;
}
void MakeRightSubTree(BTreeNode* main, BTreeNode* sub)
{
DeleteTree(main->right);
main->right = sub;
}
void ChangeLeftSubTree(BTreeNode* main, BTreeNode* sub)
{
main->left = sub;
}
void ChangeRightSubTree(BTreeNode* main, BTreeNode* sub)
{
main->right = sub;
}
void DeleteTree(BTreeNode* bt)
{
if (bt != NULL)
{
BTreeNode* delNodeRight = bt->right;
DeleteTree(bt->left);
printf("%d 을(를) 삭제합니다.\n", GetData(bt));
free(bt);
DeleteTree(delNodeRight);
}
}
void PreorderTraversal(BTreeNode* bt, Action act)
{
if (bt != NULL)
{
act(bt);
PreorderTraversal(bt->left, act);
PreorderTraversal(bt->right, act);
}
}
void InorderTraversal(BTreeNode* bt, Action act)
{
if (bt != NULL)
{
InorderTraversal(bt->left, act);
act(bt);
InorderTraversal(bt->right, act);
}
}
void PostorderTraversal(BTreeNode* bt, Action act)
{
if (bt != NULL)
{
PostorderTraversal(bt->left, act);
PostorderTraversal(bt->right, act);
act(bt);
}
}//BinarySearchTree.h 헤더 파일로 저장
//수정 날짜 : 2020.03.23
//작성자 : KOEY
#ifndef BINARYSEARCHTREE_H
#define BINARYSEARCHTREE_H
#include "BinaryTree.h"
typedef BTData BSTData;
void BSTMakeAndInit(BTreeNode** pRoot); //BST의 생성 및 초기화
BSTData BSTGetNodeData(BTreeNode* bst); //노드에 저장된 데이터 반환
void BSTInsert(BTreeNode** pRoot, BSTData data); //BST를 대상으로 데이터 저장(노드의 생성 과정 포함)
BTreeNode* BSTSearch(BTreeNode* bst, BSTData target); //BST를 대상으로 데이터 탐색, 노드 주소 반환
BTreeNode* BSTGetParentNode(BTreeNode* root, BTreeNode* bst); //첫 번째 인자를 루트 노드로 하는 트리에서 두 번째 인자로 전달한 노드의 부모 노드의 주소를 반환
BTreeNode* BSTGetMaxNode(BTreeNode* bst); //인자로 전달한 노드를 루트 노드로 하는 트리에서 가장 큰 값을 가지는 노드 주소 반환
BTreeNode* BSTGetMinNode(BTreeNode* bst); //인자로 전달한 노드를 루트 노드로 하는 트리에서 가장 작은 값을 가지는 노드 주소 반환
void BSTRemove(BTreeNode** pRoot, BSTData target); //데이터를 인자로 주어 해당 노드 삭제
void BSTShowAllData(BTreeNode* bst); //인자로 전달한 노드를 루트 노드로 하는 트리의 모든 데이터 출력(오름차순)
#endif//BinarySearchTree.c 소스 파일로 저장
//수정 날짜 : 2020.03.23
//작성자 : KOEY
#include "BinarySearchTree.h"
#include <stdio.h>
#include <stdlib.h>
#define LEFT -1
#define RIGHT 1
void BSTMakeAndInit(BTreeNode** pRoot)
{
*pRoot = NULL;
}
BSTData BSTGetNodeData(BTreeNode* bst)
{
return GetData(bst);
}
void BSTInsert(BTreeNode** pRoot, BSTData data)
{
BTreeNode* parentNode = NULL; //currentNode의 부모 노드를 저장할 변수
BTreeNode* currentNode = *pRoot;
while (currentNode != NULL)
{
if (GetData(currentNode) == data) //같은 키 값이 저장되는 것을 방지
{
return;
}
parentNode = currentNode;
if (data < GetData(currentNode))
{
currentNode = GetLeftSubTree(currentNode); //currentNode 값을 왼쪽 자식 노드의 주소로 변경
}
else
{
currentNode = GetRightSubTree(currentNode); //currentNode 값을 오른쪽 자식 노드의 주소로 변경
}
}
BTreeNode* newNode = MakeBTreeNode();
SetData(newNode, data);
if (parentNode == NULL) //parentNode가 NULL이라는 것은 currentNode가 루트 노드라는 의미
{
*pRoot = newNode;
}
else
{
if (data < GetData(parentNode))
{
MakeLeftSubTree(parentNode, newNode);
}
else
{
MakeRightSubTree(parentNode, newNode);
}
}
}
BTreeNode* BSTSearch(BTreeNode* bst, BSTData target)
{
BTreeNode* currentNode = bst;
while (GetData(currentNode) != target)
{
if (target < currentNode->data)
{
currentNode = GetLeftSubTree(currentNode);
}
else
{
currentNode = GetRightSubTree(currentNode);
}
if (currentNode == NULL)
{
return NULL;
}
}
return currentNode;
}
BTreeNode* BSTGetParentNode(BTreeNode* root, BTreeNode* bst) //인자로 전달한 노드의 부모 노드의 주소를 반환
{
BTreeNode* parentNode = NULL;
BTreeNode* currentNode = root;
while (currentNode != bst)
{
parentNode = currentNode;
currentNode = (GetData(currentNode) < GetData(bst)) ? currentNode->right : currentNode->left;
}
return parentNode;
}
BTreeNode* BSTGetMaxNode(BTreeNode* bst)
{
BTreeNode* maxNode = bst;
while (GetRightSubTree(maxNode) != NULL) //maxNode의 오른쪽 자식 노드가 존재 한다면
{
maxNode = GetRightSubTree(maxNode);
}
return maxNode;
}
BTreeNode* BSTGetMinNode(BTreeNode* bst)
{
BTreeNode* minNode = bst;
while (GetLeftSubTree(minNode) != NULL) //minNode의 왼쪽 자식 노드가 존재 한다면
{
minNode = GetLeftSubTree(minNode);
}
return minNode;
}
BTreeNode* GetAlternateNode(BTreeNode* delNode) //인자로 전달한 노드를 대체할 노드를 반환하고, 대체 노드의 부모가 대체 노드 대신 NULL을 가리키게 하는 함수
{
BTreeNode* alternateNode; //대체 노드를 저장할 변수
BTreeNode* parentNode; //대체 노드의 부모를 저장할 변수
if (GetLeftSubTree(delNode) != NULL) //삭제할 노드의 왼쪽 자식 노드가 존재하면
{
alternateNode = BSTGetMaxNode(GetLeftSubTree(delNode)); //삭제할 노드의 왼쪽 자식 노드를 대체 노드로 설정
parentNode = BSTGetParentNode(delNode, alternateNode); //대체 노드의 부모 노드 저장
if (parentNode == delNode) //부모 노드가 삭제할 노드라면
{
parentNode->left = NULL; //대체 노드는 부모 노드의 왼쪽 자식이므로 왼쪽을 NULL로 변경
}
else //부모 노드가 삭제할 노드가 아니라면
{
parentNode->right = NULL; //대체 노드는 부모 노드의 오른쪽 자식이므로 오른쪽을 NULL로 변경
}
}
else if (GetRightSubTree(delNode) != NULL) //삭제할 노드의 오른쪽 자식 노드가 존재하면
{
alternateNode = BSTGetMinNode(GetRightSubTree(delNode)); //삭제할 노드의 오른쪽 자식 노드를 대체 노드로 설정
parentNode = BSTGetParentNode(delNode, alternateNode);
if (parentNode == delNode)
{
parentNode->right = NULL;
}
else
{
parentNode->left = NULL;
}
}
else //자식 노드가 존재하지 않으면
{
return NULL; //대체 노드는 NULL 반환
}
return alternateNode;
}
void BSTRemove(BTreeNode** pRoot, BSTData target)
{
BTreeNode* removeNode = BSTSearch(*pRoot, target); //삭제할 노드 저장
if (removeNode == NULL) //삭제할 노드가 없다면
{
return; //함수 종료
}
BTreeNode* parentNode = BSTGetParentNode(*pRoot, removeNode); //삭제할 노드의 부모 노드 저장
BTreeNode* alternateNode = GetAlternateNode(removeNode); //대체 노드를 찾고 대체 노드의 부모 노드가 대체 노드 대신 NULL을 가리키도록 함
if (parentNode != NULL) //부모 노드가 존재한다면
{
if (GetLeftSubTree(parentNode) == removeNode) //삭제할 노드가 부모 노드의 왼쪽 자식 노드라면
{
parentNode->left = alternateNode; //부모 노드가 삭제할 노드 대신 대체 노드를 가리키도록 함
}
else //삭제할 노드가 부모 노드의 오른쪽 자식 노드라면
{
parentNode->right = alternateNode; //부모 노드가 삭제할 노드 대신 대체 노드를 가리키도록 함
}
}
else //부모 노드가 존재하지 않는다면, 즉, 삭제할 노드가 루트 노드라면
{
*pRoot = alternateNode; //루트 노드의 주소를 대체 노드의 주소로 바꿈
}
if (alternateNode == NULL) //대체 노드가 존재하지 않는다면
{
free(removeNode); //삭제할 노드 삭제
return;
}
BSTGetMinNode(alternateNode)->left = removeNode->left; //삭제할 노드의 왼쪽 자식 노드를, 대체 노드를 루트 노드로 하는 서브 트리에서 가장 작은 값을 가지는 노드의 왼쪽 자식 노드로 연결
BSTGetMaxNode(alternateNode)->right = removeNode->right; //삭제할 노드의 오른쪽 자식 노드를, 대체 노드를 루트 노드로 하는 서브 트리에서 가장 큰 값을 가지는 노드의 오른쪽 자식 노드로 연결
free(removeNode); //삭제할 노드 삭제
}
void BSTShowAllData(BTreeNode* bst) //인자로 전달한 노드를 루트 노드로 하는 트리의 모든 데이터 출력(오름차순)
{
if (bst == NULL) return;
BSTShowAllData(bst->left);
printf("%d ", GetData(bst));
BSTShowAllData(bst->right);
}루트 노드를 기준으로 왼쪽과 오른쪽의 균형이 잘 잡혀 있는 이진 탐색 트리가 있다고 가정할 때, 이 균형이 깨지게 되는 때가 언제일지 생각해 봅니다. 이진 탐색 트리의 균형이 깨지게 되는 때는 바로 새로운 데이터를 저장하거나, 데이터를 삭제할 때입니다. 따라서 우리는 데이터를 추가하거나 확장하는 과정에서만 균형이 맞는지 검사하고 리밸런싱 하면 됩니다. 따라서 트리의 균형을 리밸런싱 하는 함수의 이름이 Rebalance일 때, 데이터를 추가하거나 삭제하는 두 함수는 다음과 같이 확장되어야 합니다.
void BSTInsert(BTreeNode** pRoot, BSTData data)
{
......
Rebalance(pRoot);
}
BTreeNode* BSTRemove(BTreeNode* pRoot, BSTData target)
{
......
Rebalance(pRoot);
return delNode;
}리밸런싱을 하기 위해서는 우선 트리의 균형 상태를 알 수 있어야 합니다. 물론 불균형의 여부는 루트 노드를 기준으로 판단합니다. 트리의 균형 여부는 균형 인수를 통해서 알 수 있습니다. 그리고 균형 인수는 왼쪽 서브 트리의 높이와 오른쪽 서브 트리의 높이를 알아야 계산할 수 있습니다. 따라서 우리는 트리의 높이를 계산하는 함수를 먼저 정의해야 합니다.
트리의 높이를 반환하는 함수는 다음과 같이 정의할 수 있습니다..
int GetHeight(BTreeNode* bst)
{
if (bst == NULL) return 0;
int left = 0, right = 0;
left = GetHeight(GetLeftSubTree(bst));
right = GetHeight(GetRightSubTree(bst));
return (left > right) ? left + 1 : right + 1;
}트리의 높이를 구했으면 이를 이용해 균형 인수를 계산해야 합니다. 균형 인수를 계산하는 함수는 다음과 같습니다.
int GetHeighrDiff(BTreeNode* bst)
{
if (bst == NULL) return 0;
int left = GetHeight(GetLeftSubTree(bst));
int right = GetHeight(GetRightSubTree(bst));
return left - right;
}이제 균형 인수까지 구했으므로 트리의 불균형 상태를 알 수 있습니다. 불균형 상태를 알았으면 이제 리밸런싱 할 차례입니다. 리밸런싱은 LL회전, RR회전, LR회전, RL회전의 방법을 사용합니다. 그리고 이들은 이전에 함수들로 구현한 적 있습니다. 이전에 구현했던 리밸런싱 함수들을 다시 보이겠습니다.
BTreeNode* LLRotate(BTreeNode* bst)
{
BTreeNode* parentNode = bst;
BTreeNode* childNode = GetLeftSubTree(bst);
ChangeLeftSubTree(parentNode, GetRightSubTree(childNode));
ChangeRightSubTree(childNode, parentNode);
return childNode;
}
BTreeNode* RRRotate(BTreeNode* bst)
{
BTreeNode* parentNode = bst;
BTreeNode* childNode = GetRightSubTree(bst);
ChangeRightSubTree(parentNode, GetLeftSubTree(childNode));
ChangeLeftSubTree(childNode, parentNode);
return childNode;
}
BTreeNode* LRRotate(BTreeNode* bst)
{
BTreeNode* parentNode = bst;
BTreeNode* childNode = GetLeftSubTree(bst);
ChangeLeftSubTree(parentNode, RRRotate(childNode));
LLRotate(parentNode);
return childNode;
}
BTreeNode* RLRotate(BTreeNode* bst)
{
BTreeNode* parentNode = bst;
BTreeNode* childNode = GetRightSubTree(bst);
ChangeRightSubTree(parentNode, LLRotate(childNode));
RRRotate(parentNode);
return childNode;
}이제 이들을 이용해 Rebalance 함수를 정의해 보겠습니다. 이 함수는 AVL 트리의 불균형 유무를 판단하고, 적절한 리밸런싱 과정을 적용하는 함수가 됩니다.
BTreeNode* Rebalance(BTreeNode** pRoot)
{
int heightDiff = GetHeighrDiff(*pRoot);
if (heightDiff >= 2) //균형 인수가 2 이상이면 LL 혹은 LR
{
heightDiff = GetHeighrDiff(GetLeftSubTree(*pRoot)); //왼쪽 자식 노드의 균형 인수 저장
if (heightDiff >= 0) //왼쪽 자식 노드의 균형 인수가 0 이상이면 LL
{
*pRoot = LLRotate(*pRoot);
}
else
{
*pRoot = LRRotate(*pRoot);
}
}
else if (heightDiff <= -2) //균형 인수가 -2 이하면 RR 혹은 RL
{
heightDiff = GetHeighrDiff(GetRightSubTree(*pRoot)); //오른쪽 자식 노드의 균형 인수 저장
if (heightDiff <= 0) //오른쪽 자식 노드의 균형 인수가 0 이하면 RR
{
*pRoot = RRRotate(*pRoot);
}
else
{
*pRoot = RLRotate(*pRoot);
}
}
return *pRoot;
}이렇게 리밸런싱에 필요한 모든 함수들을 구현했습니다. 이들 함수들이 어느 파일에 어떻게 선언되고, 정의되었는지 보이겠습니다.
//AVLRebalance.h 헤더 파일로 저장
//수정 날짜 : 2020.03.23
//작성자 : KOEY
#ifndef AVL_REBALANCE_H
#define AVL_REBALANCE_H
#include "BinaryTree.h"
int GetHeight(BTreeNode* bst); //트리의 높이를 반환, 루트 노드를 인자로 전달
int GetHeighrDiff(BTreeNode* bst); //루트 노드의 균형 인수 반환, 루트 노드를 인자로 전달
BTreeNode* LLRotate(BTreeNode* bst); //LL회전 함수, 루트 노드를 인자로 전달
BTreeNode* RRRotate(BTreeNode* bst); //RR회전 함수, 루트 노드를 인자로 전달
BTreeNode* LRRotate(BTreeNode* bst); //LR회전 함수, 루트 노드를 인자로 전달
BTreeNode* RLRotate(BTreeNode* bst); //RL회전 함수, 루트 노드를 인자로 전달
BTreeNode* Rebalance(BTreeNode** pRoot); //리밸런싱 함수, 루트 노드의 주소를 인자로 전달
#endif //AVLRebalance.c 소스 파일로 저장
//수정 날짜 : 2020.03.23
//작성자 : KOEY
#include "AVLRebalance.h"
#include <stdio.h>
int GetHeight(BTreeNode* bst)
{
if (bst == NULL) return 0;
int left = 0, right = 0;
left = GetHeight(GetLeftSubTree(bst));
right = GetHeight(GetRightSubTree(bst));
return (left > right) ? left + 1 : right + 1;
}
int GetHeighrDiff(BTreeNode* bst)
{
if (bst == NULL) return 0;
int left = GetHeight(GetLeftSubTree(bst));
int right = GetHeight(GetRightSubTree(bst));
return left - right;
}
BTreeNode* LLRotate(BTreeNode* bst)
{
BTreeNode* parentNode = bst;
BTreeNode* childNode = GetLeftSubTree(bst);
ChangeLeftSubTree(parentNode, GetRightSubTree(childNode));
ChangeRightSubTree(childNode, parentNode);
return childNode;
}
BTreeNode* RRRotate(BTreeNode* bst)
{
BTreeNode* parentNode = bst;
BTreeNode* childNode = GetRightSubTree(bst);
ChangeRightSubTree(parentNode, GetLeftSubTree(childNode));
ChangeLeftSubTree(childNode, parentNode);
return childNode;
}
BTreeNode* LRRotate(BTreeNode* bst)
{
BTreeNode* parentNode = bst;
BTreeNode* childNode = GetLeftSubTree(bst);
ChangeLeftSubTree(parentNode, RRRotate(childNode));
LLRotate(parentNode);
return childNode;
}
BTreeNode* RLRotate(BTreeNode* bst)
{
BTreeNode* parentNode = bst;
BTreeNode* childNode = GetRightSubTree(bst);
ChangeRightSubTree(parentNode, LLRotate(childNode));
RRRotate(parentNode);
return childNode;
}
BTreeNode* Rebalance(BTreeNode** pRoot)
{
int heightDiff = GetHeighrDiff(*pRoot);
if (heightDiff >= 2) //균형 인수가 2 이상이면 LL 혹은 LR
{
heightDiff = GetHeighrDiff(GetLeftSubTree(*pRoot)); //왼쪽 자식 노드의 균형 인수 저장
if (heightDiff >= 0) //왼쪽 자식 노드의 균형 인수가 0 이상이면 LL
{
*pRoot = LLRotate(*pRoot);
}
else
{
*pRoot = LRRotate(*pRoot);
}
}
else if (heightDiff <= -2) //균형 인수가 -2 이하면 RR 혹은 RL
{
heightDiff = GetHeighrDiff(GetRightSubTree(*pRoot)); //오른쪽 자식 노드의 균형 인수 저장
if (heightDiff <= 0) //오른쪽 자식 노드의 균형 인수가 0 이하면 RR
{
*pRoot = RRRotate(*pRoot);
}
else
{
*pRoot = RLRotate(*pRoot);
}
}
return *pRoot;
}아직 끝난 것은 아닙니다. 우리는 Rebalance 함수를 이제 막 구현했을 뿐입니다. 우리가 Rebalance 함수를 구현한 이유는 AVL 트리에서 데이터를 저장하거나 삭제할 때 균형이 무너지는 것을 방지하기 위함입니다. 이제 ReBalance 함수를 BSTInsert 함수와 BSTRemove 함수에 추가해서 두 함수를 확장해야 합니다. 다음은 확장된 두 함수입니다.
void BSTInsert(BTreeNode** pRoot, BSTData data)
{
BTreeNode* parentNode = NULL; //currentNode의 부모 노드를 저장할 변수
BTreeNode* currentNode = *pRoot;
while (currentNode != NULL)
{
if (GetData(currentNode) == data) //같은 키 값이 저장되는 것을 방지
{
return;
}
parentNode = currentNode;
if (data < GetData(currentNode))
{
currentNode = GetLeftSubTree(currentNode); //currentNode 값을 왼쪽 자식 노드의 주소로 변경
}
else
{
currentNode = GetRightSubTree(currentNode); //currentNode 값을 오른쪽 자식 노드의 주소로 변경
}
}
BTreeNode* newNode = MakeBTreeNode();
SetData(newNode, data);
if (parentNode == NULL) //parentNode가 NULL이라는 것은 currentNode가 루트 노드라는 의미
{
*pRoot = newNode;
}
else
{
if (data < GetData(parentNode))
{
MakeLeftSubTree(parentNode, newNode);
}
else
{
MakeRightSubTree(parentNode, newNode);
}
}
*pRoot = Rebalance(pRoot); //리밸런싱 추가
}void BSTRemove(BTreeNode** pRoot, BSTData target)
{
BTreeNode* removeNode = BSTSearch(*pRoot, target); //삭제할 노드 저장
if (removeNode == NULL) //삭제할 노드가 없다면
{
return; //함수 종료
}
BTreeNode* parentNode = BSTGetParentNode(*pRoot, removeNode); //삭제할 노드의 부모 노드 저장
BTreeNode* alternateNode = GetAlternateNode(removeNode); //대체 노드를 찾고 대체 노드의 부모 노드가 대체 노드 대신 NULL을 가리키도록 함
if (parentNode != NULL) //부모 노드가 존재한다면
{
if (GetLeftSubTree(parentNode) == removeNode) //삭제할 노드가 부모 노드의 왼쪽 자식 노드라면
{
parentNode->left = alternateNode; //부모 노드가 삭제할 노드 대신 대체 노드를 가리키도록 함
}
else //삭제할 노드가 부모 노드의 오른쪽 자식 노드라면
{
parentNode->right = alternateNode; //부모 노드가 삭제할 노드 대신 대체 노드를 가리키도록 함
}
}
else //부모 노드가 존재하지 않는다면, 즉, 삭제할 노드가 루트 노드라면
{
*pRoot = alternateNode; //루트 노드의 주소를 대체 노드의 주소로 바꿈
}
if (alternateNode == NULL) //대체 노드가 존재하지 않는다면
{
free(removeNode); //삭제할 노드 삭제
*pRoot = Rebalance(pRoot); //리밸런싱 추가
return;
}
BSTGetMinNode(alternateNode)->left = removeNode->left;
BSTGetMaxNode(alternateNode)->right = removeNode->right;
free(removeNode); //삭제할 노드 삭제
*pRoot = Rebalance(pRoot); //리밸런싱 추가
}이제 AVL 트리가 리밸런싱을 제대로 하고 있는지 확인할 차례입니다. 다음과 같이 main 함수를 작성하고 그 실행결과를 확인합니다.
//main.c 소스 파일로 저장
#include <stdio.h>
#include "BinarySearchTree.h"
int main(void)
{
BTreeNode* avlRoot;
BTreeNode* currentLeftNode;
BTreeNode* currentRightNode;
BSTMakeAndInit(&avlRoot);
BSTInsert(&avlRoot, 1);
BSTInsert(&avlRoot, 2);
BSTInsert(&avlRoot, 3);
BSTInsert(&avlRoot, 4);
BSTInsert(&avlRoot, 5);
BSTInsert(&avlRoot, 6);
BSTInsert(&avlRoot, 7);
BSTInsert(&avlRoot, 8);
BSTInsert(&avlRoot, 9);
BSTInsert(&avlRoot, 10);
printf("루트 노드 : %d\n", GetData(avlRoot));
currentLeftNode = GetLeftSubTree(avlRoot);
currentRightNode = GetRightSubTree(avlRoot);
printf("왼쪽 1 : %d, 오른쪽 1 : %d\n", GetData(currentLeftNode), GetData(currentRightNode));
currentLeftNode = GetLeftSubTree(currentLeftNode);
currentRightNode = GetRightSubTree(currentRightNode);
printf("왼쪽 2 : %d, 오른쪽 2 : %d\n", GetData(currentLeftNode), GetData(currentRightNode));
currentLeftNode = GetLeftSubTree(currentLeftNode);
currentRightNode = GetRightSubTree(currentRightNode);
printf("왼쪽 3 : %d, 오른쪽 3 : %d\n", GetData(currentLeftNode), GetData(currentRightNode));
return 0;
}
/*
실행결과
루트 노드 : 5
왼쪽 1 : 4, 오른쪽 1 : 6
왼쪽 2 : 3, 오른쪽 2 : 7
왼쪽 3 : 2, 오른쪽 3 : 8
*/위의 main 함수는 1부터 10까지 순서대로 값을 입력하고 있습니다. 그래서 만약 리밸런싱을 하지 않는다면 위의 이진 탐색 트리는 오른쪽 자식 노드만 가지는 매우 불균형한 트리가 되었을 것입니다. 하지만 실행결과 리밸런싱이 제대로 수행되어 루트 노드는 5가 되었고 균형이 갖춰진 모습입니다.
하지만 이렇게 완성한 AVL 트리도 완전히 균형잡힌 트리는 아닙니다. 왜냐하면 다음과 같은 트리는 분명 리밸런싱이 필요한 불균형한 트리지만 우리가 구현한 AVL 트리는 이를 리밸런싱 하지 않습니다. 루트 노드에 대해서만 리밸런싱을 수행하기 때문입니다.
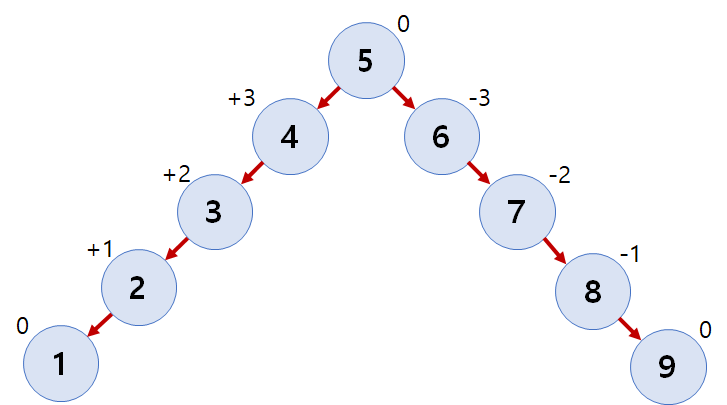
이런 문제를 어떻게 해결할 수 있을지 생각해 보는 것도 재밌을 것 같습니다.