티스토리 뷰
주의 사항!
- 이 글은 제가 직접 공부하는 중에 작성되고 있습니다.
- 따라서 제가 이해하는 그대로의 내용이 포함됩니다.
- 따라서 이 글은 사실과는 다른 내용이 포함될 수 있습니다.
사실 트리는 그래프의 한 유형입니다. 다음 그래프를 보겠습니다.
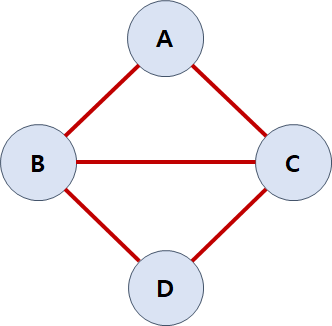
위 그래프의 정점 A로부터 D로 가는 경로들을 찾아보면 다음과 같이 찾을 수 있습니다.
- A - B - D
- A - C - D
- A - B - C - D
- A - C - B - D
이렇듯 두 개의 정점을 잇는 간선을 순서대로 나열한 것을 가리켜 '경로'라고 합니다. 그리고 위의 네 경로와 같이 동일한 간선을 중복하여 포함하지 않는 경로를 가리켜 '단순 경로'라고 합니다. 정점 A에서 D로 이르는, 단순 경로가 아닌 경로를 찾으면 다음과 같은 경로를 찾을 수 있습니다.
- A - B - C - A - B - D
위 경로는 정점 A와 B를 잇는 간선을 중복 포함합니다. 혹시나 해서 설명하자면, 다음과 같은 경로는 단순 경로에 해당됩니다.
- A - B - C - A
정점 A를 중복해서 가지지만, 중복된 간선은 없기 때문입니다. 그리고 이렇듯 단순 경로이면서 시작과 끝이 같은 경로를 가리켜 '사이클'이라고 합니다. 따라서 다음의 그래프들은 사이클을 이루지 않습니다.

그런데 위의 그래프들은 그래프이자 트리입니다. 위 그래프들을 조금씩 돌려보면 트리임을 쉽게 눈치챌 수 있습니다.
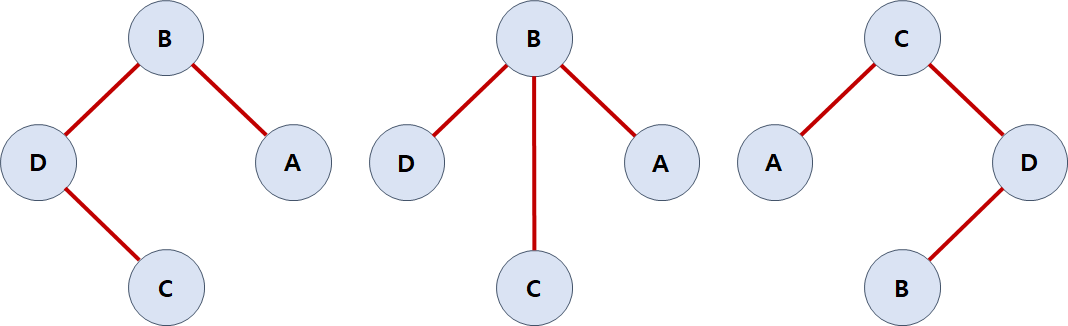
그리고 위 그래프와 같이 사이클을 형성하지 않는 그래프들을 가리켜 '신장 트리'라고 합니다.
신장 트리의 특징 두 가지는 다음과 같습니다.
- 그래프의 모든 정점이 간선에 의해서 하나로 연결되어 있다.
- 그래프 내에서 사이클을 형성하지 않는다.
앞선 예에서는 무방향 그래프를 대상으로 신장 트리의 예를 들었지만, 가중치 그래프와 방향 그래프를 대상으로도 신장 트리를 구성할 수 있습니다. 그리고 가중치 그래프를 대상으로 신장 트리를 구성했을 때, 모든 간선의 가중치 합이 최소인 신장 트리를 가리켜 '최소 비용 신장 트리' 혹은 '최소 신장 트리'라고 하며, 줄여서 MST라고 부르기도 합니다.
즉, 다음과 같은 가중치 그래프가 있을 때,

최소 비용 신장 트리는 다음과 같습니다.

이쯤 되면 최소 비용 신장 트리(MST)가 어떠한 형태로 활용될 수 있을지 눈치챌 수 있을 것입니다. MST를 활용하면 기차, 지하철, 버스 등의 노선을 통해 어떤 목적지로 가는 가장 빠른 경로를 찾을 수 있습니다. 또 전기회로의 구성이나 네트워크의 구축과 관련된 문제의 답을 구하는 데에도 활용할 수 있습니다.
최소 비용 신장 트리의 구성에 사용되는 대표적인 알고리즘 두 가지는 다음과 같습니다.
- 크루스칼 알고리즘
- 프림 알고리즘
크루스칼 알고리즘은 가중치를 기준으로 간선을 정렬한 후에, MST가 될 때까지 간선을 하나씩 선택 또는 삭제해 나가는 방식을 사용합니다. 반면 프림 알고리즘은 하나의 정점을 시작으로 MST가 될 때까지 트리를 확장해 나가는 방식을 사용합니다. 물론 이 두 가지 외에도 다른 알고리즘이 더 있지만 이 책에서는 MST를 보다 더 대표하는 크루스칼 알고리즘을 선택해서 설명합니다.
크루스칼 알고리즘의 핵심은 간선들을 가중치를 기준으로 정렬한다는 것입니다. 크루스칼 알고리즘은 다음과 같은 과정을 거쳐 진행됩니다. 먼저, 다음과 같은 그래프가 있다고 가정하겠습니다.

위 그래프의 간선들을 가중치를 기준으로 오름차순으로 정렬하면 다음과 같습니다.
2, 3, 4, 6, 7, 8, 11, 12, 13
이제 가장 작은 값의 간선부터 하나씩 선택해가며 MST를 완성합니다.
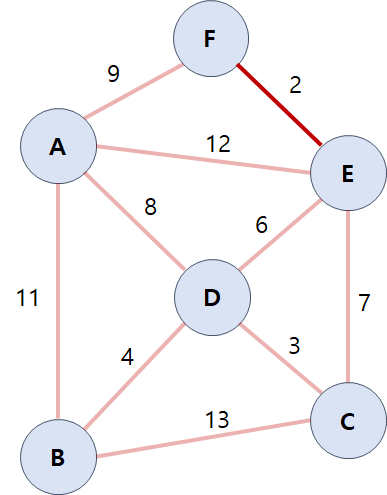
가장 작은 가중치 2를 가지는 간선을 선택한 모습입니다. 이어서 3, 4, 6을 가중치로 가지는 간선들도 선택하면 다음과 같이 됩니다.

이어서 7을 가중치로 가지는 간선을 선택하고자 합니다. 그런데 해당 간선을 선택하면 정점 C, D, E가 서로 연결되어 사이클을 이루게 됩니다. 신장 트리는 사이클을 이루면 안 되기 때문에 간선 7은 선택할 수 없습니다. 따라서 7은 건너뛰고 8부터 선택과정을 이어갑니다.
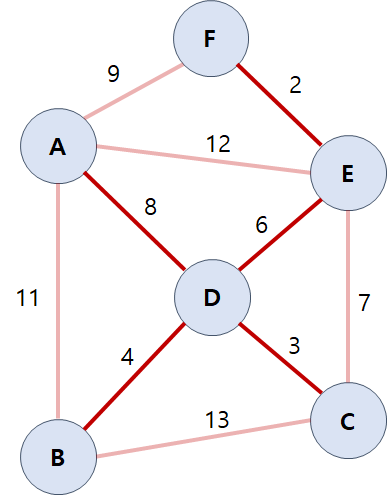
8을 가중치로 가지는 간선까지 선택 완료했습니다. 그리고 여기까지 해서 최소 비용 신장 트리가 완성되었습니다. 선택되지 않은 간선들을 제외하면 다음과 같이 됩니다.

최소 비용 신장 트리가 완성됐는지 여부는 정점의 수와 간선의 수를 비교하여 확인할 수 있습니다. 간선의 수가 정점의 수보다 하나 적으면 최소 비용 신장 트리가 완성되었다고 봅니다.
크루스칼 알고리즘은 간선을 오름차순으로만 정렬하지는 않습니다. 내림차순으로 정렬하고 가장 가중치가 높은 간선부터 하나씩 제외시켜가는 방식으로 MST를 완성할 수도 있습니다.
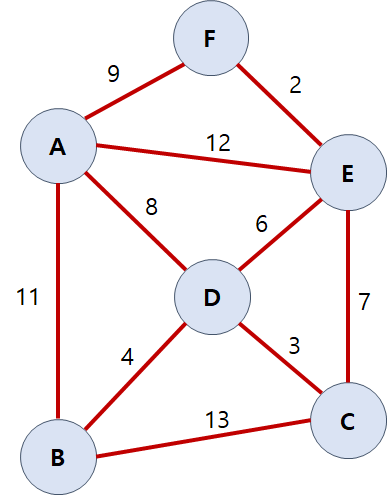
아까와 같은 그래프가 있습니다. 간선들을 내림차순으로 정렬하고, 가중치가 가장 큰 간선부터 하나씩 제외해 나갑니다. 먼저 가중치 13을 가지는 간선을 제외하면 다음과 같이 됩니다.

이어서 12, 11, 9도 제외시키면 다음과 같습니다.
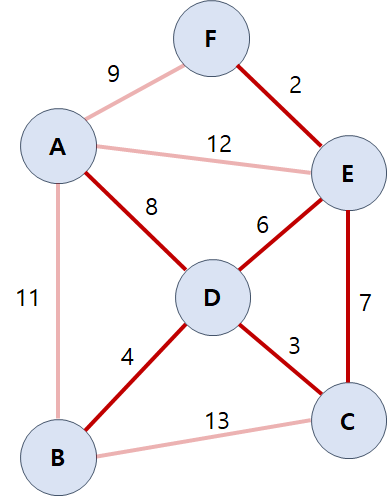
다음은 가중치 8을 가지는 간선 차례입니다. 그런데 해당 간선을 제외하면 정점 A에는 연결된 간선이 하나도 남지 않게 됩니다. 신장 트리는 모든 정점들이 간선에 의해서 하나로 연결되어 있어야 하기 때문에 해당 간선을 제외할 수는 없습니다. 따라서 가중치 8을 가지는 간선은 건너뛰고 7부터 다시 제외시킵니다.
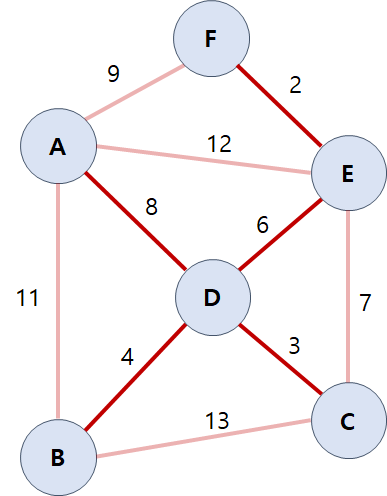
가중치 7을 가지는 간선까지 제외하고 나면 MST가 완성됩니다. 오름차순으로 정렬했던 것과 마찬가지로 간선의 수가 정점의 수보다 하나 적으면 MST가 완성되었다고 봅니다.
이제 크루스칼 알고리즘을 직접 구현해볼 차례입니다. 이번에 구현하게 될 크루스칼 알고리즘은 가중치를 기준으로 간선을 내림차순으로 정렬한 다음 높은 가중치의 간선부터 시작해서 하나씩 제거하는 방식으로 구현하게 됩니다. 이를 위해서 앞서 구현했던 ALGraphBFS.h 파일과 ALGraphBFS.c 파일을 활용하고자 합니다. 그리고 BFS를 구현하는 데에 사용했던 연결 리스트 파일과 큐 파일도 같이 사용하게 됩니다.
크루스칼 알고리즘의 구현을 위해서는 먼저 그래프를 구성해야 하기 때문에 앞서 구현했던 ALGraphBFS.h 헤더 파일과 소스 파일을 사용합니다. 하지만 이번에는 가중치 그래프를 구성해야 하기 때문에 이들 파일을 확장하여 다음과 같은 파일을 새로 만들어 사용합니다.
- ALGraphKruskal.h
- ALGraphKruskal.c
또, 크루스칼 알고리즘을 구현하려면, 어느 간선을 삭제했을 때, 이 간선에 의해 연결되어 있던 정점들이 다른 간선을 통해서도 연결되는지 확인할 수 있어야 합니다. 따라서 이 기능을 제공하는 함수를 구현해야 합니다.
그리고 크루스칼 알고리즘의 구현을 위해서는 간선들을 가중치를 기준으로 정렬할 수 있어야 하는데. 이를 위해서 힙(우선순위 큐)을 사용할 것입니다. 그리고 가중치 그래프의 표현을 위해서는 가중치가 포함된 간선의 정보를 담을 수 있어야 합니다. 따라서 간선이 연결하는 두 정점과 가중치의 정보를 가지는 구조체의 정의를 위해 다음의 헤더 파일을 추가합니다.
- ALEdge.h
우선은 간선의 정보를 저장할 구조체를 정의할 ALEdge.h 헤더 파일을 소개합니다.
//ALEdge.h
//수정날짜 : 2021.03.29
//작성자 : KOEY
#ifndef AL_EDGE_H
#define AL_EDGE_H
typedef struct Edge
{
int vertex1; //간선이 연결하는 첫 번째 정점
int vertex2; //간선이 연결하는 두 번째 정점
int weight; //간선의 가중치
}Edge;
#endifEdge는 간선을 의미하며, vertex1과 vertex2는 각각 간선이 연결하는 두 정점을 의미합니다. 그리고 weight은 가중치를 의미합니다.
이제 이 간선을 저장할 힙을 정의하고자 합니다. 저는 힙이라고 부르고 있지만 정확히는 우선순위 큐를 이용하는 것입니다. 다만, 저는 둘의 차이점을 명확히 구분하기 어려워서 힙을 사용합니다.
//Heap.h
//수정날짜 : 2021.03.29
//작성자 : KOEY
#ifndef HEAP_H
#define HEAP_H
#include "ALEdge.h"
#define TRUE 1
#define FALSE 0
#define ARR_LEN 100
typedef Edge HData;
typedef struct HeapElem
{
HData data;
}HeapElem;
typedef int(*SortFunc)(HData d1, HData d2);
typedef struct Heap
{
int numOfData;
HeapElem heapArr[ARR_LEN];
SortFunc Sort;
}Heap;
void HeapInit(Heap* ph, SortFunc func) ;
int HeapIsEmpty(Heap* ph);
void HInsert(Heap* ph, HData data);
HData HDelete(Heap* ph);
void SetSortRule(Heap* ph, SortFunc func);
#endif위 헤더 파일을 보면,
#include "ALEdge.h"앞서 정의했던 ALEdge.h 파일을 인클루드 하고 있습니다.
typedef Edge HData;간선을 데이터로 가지며,
typedef struct Heap
{
int numOfData;
HeapElem heapArr[ARR_LEN];
SortFunc Sort;
}Heap;배열 기반으로 힙을 구현했습니다. 앞선 시간에서 힙은 배열을 이용해 구현하는 것이 원칙으로 여겨진다고 소개했습니다. 그리고 데이터를 정렬할 함수 포인터도 멤버로 가집니다. 정렬 함수를 따로 선언하여 오름차순으로 정렬할지, 내림차순으로 정렬할지 결정할 수 있습니다.
다음은 힙의 소스 파일입니다.
//Heap.c
//수정날짜 : 2021.03.29
//작성자 : KOEY
#include "Heap.h"
void HeapInit(Heap* ph, SortFunc func)
{
ph->numOfData = 0;
ph->Sort = func;
}
int HeapIsEmpty(Heap* ph)
{
return (ph->numOfData == 0) ? TRUE : FALSE;
}
void HInsert(Heap* ph, HData data)
{
ph->numOfData++;
int currentIndex = ph->numOfData;
int parentIndex = currentIndex / 2;
HData parent = ph->heapArr[parentIndex].data;
while (parentIndex >= 1 && ph->Sort(data, parent))
{
ph->heapArr[currentIndex].data = parent;
currentIndex = parentIndex;
parentIndex = currentIndex / 2;
parent = ph->heapArr[parentIndex].data;
}
ph->heapArr[currentIndex].data = data;
}
int GetFirstchildIndex(Heap* ph, int currentIndex)
{
int leftIndex = currentIndex * 2;
int rightIndex = leftIndex + 1;
if (rightIndex > ph->numOfData)
{
if (leftIndex > ph->numOfData)
{
return -1; //자식이 없음을 의미
}
else
{
return leftIndex;
}
}
else
{
return (ph->Sort(ph->heapArr[leftIndex].data, ph->heapArr[rightIndex].data)) ? leftIndex : rightIndex;
}
}
HData HDelete(Heap* ph)
{
HData delData = ph->heapArr[1].data;
HData last = ph->heapArr[ph->numOfData--].data;
int currentIndex = 1;
int childIndex = GetFirstchildIndex(ph, currentIndex);
while (childIndex != -1 && ph->Sort(ph->heapArr[childIndex].data, last))
{
ph->heapArr[currentIndex].data = ph->heapArr[childIndex].data;
currentIndex = childIndex;
childIndex = GetFirstchildIndex(ph, currentIndex);
}
ph->heapArr[currentIndex].data = last;
return delData;
}
void SetSortRule(Heap* ph, SortFunc func)
{
ph->Sort = func;
}
위 파일의,
int GetFirstchildIndex(Heap* ph, int currentIndex)
{
int leftIndex = currentIndex * 2;
int rightIndex = leftIndex + 1;
if (rightIndex > ph->numOfData)
{
if (leftIndex > ph->numOfData)
{
return -1; //자식이 없음을 의미
}
else
{
return leftIndex;
}
}
else
{
return (ph->Sort(ph->heapArr[leftIndex].data, ph->heapArr[rightIndex].data)) ? leftIndex : rightIndex;
}
}위 함수는 왼쪽과 오른쪽 두 자식 중 우선순위가 앞서는 것을 찾아 해당 요소의 인덱스를 반환하는 함수입니다. 만약 자식이 존재하지 않으면 -1을 반환합니다. 이 함수는 HDelete 함수에서 호출됩니다.
이어서 ALGraphBFS.h 파일을 확장하여 작성한 ALGraphKruskal.h 헤더 파일을 소개합니다.
//ALGraphKruskal.h
//수정 날짜 : 2021.03.29
//작성자 : KOEY
#ifndef AL_GRAPH_KRUSKAL_H
#define AL_GRAPH_KRUSKAL_H
#include "LinkedList.h"
#include "Heap.h" //추가
#include "ALEdge.h" //추가
//정점의 이름을 상수화
enum { A, B, C, D, E, F, G, H, I, J, K };
typedef struct Ual
{
int numV;
int numE;
List* adjList;
int* visitInfo;
Heap heap; //추가된 변수, 간선의 가중치 정보 저장
}ALGraph;
void GraphInit(ALGraph* pg, int nv); //수정해야할 함수
void GraphDestroy(ALGraph* pg);
void AddEdge(ALGraph* pg, int fromV, int toV, int weight); //수정해야할 함수
void ShowGraphEdgeInfo(ALGraph* pg);
void BFShowGraphVertex(ALGraph* pg, int startV);
void ConKruskalMST(ALGraph* pg); //추가된 함수, 최소 비용 신장 트리 구성
void ShowGraphEdgeWeightInfo(ALGraph* pg); //추가된 함수, 가중치 정보 출력
#endif위 파일을 보면,
typedef struct Ual
{
int numV;
int numE;
List* adjList;
int* visitInfo;
Heap heap; //추가된 변수, 간선의 가중치 정보 저장
}ALGraph;여기에 힙을 저장하는 새로운 변수가 추가되었습니다. 이 힙은 간선의 정보들을 정렬하여 저장합니다. 후에 이 힙에서 간선들의 정보를 하나씩 빼서 해당 간선을 삭제할 것인지 그대로 둘 것인지를 결정합니다. 그리고 이 새로운 변수가 추가됨에 따라 수정이 필요한 함수가 생겼고, 새로 추가되는 함수도 생겼습니다.
다음은 함수들을 구현한 파일입니다.
//ALGraphDFS.c
//수정날짜 : 2021.03.27
//작성자 : KOEY
#include "ALGraphKruskal.h"
#include "LLBQueue.h"
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
int WeightComp(HData d1, HData d2)
{
return (d1.weight > d2.weight) ? TRUE : FALSE;
}
void GraphInit(ALGraph* pg, int nv)
{
pg->adjList = (List*)malloc(sizeof(List) * nv);
if (pg->adjList == NULL)
{
printf("메모리 공간이 부족합니다.\n");
exit(1);
}
int i;
for (i = 0; i < nv; i++)
{
ListInit(&(pg->adjList[i]));
}
pg->numE = 0;
pg->numV = nv;
pg->visitInfo = (int*)malloc(sizeof(int) * pg->numV);
if (pg->visitInfo == NULL)
{
printf("메모리 공간이 부족합니다. \n");
exit(1);
}
memset(pg->visitInfo, 0, sizeof(int) * pg->numV);
//추가된 부분, 힙의 초기화
HeapInit(&(pg->heap), WeightComp);
}
void GraphDestroy(ALGraph* pg)
{
if (pg->adjList == NULL)
{
return;
}
int i;
for (i = 0; i < pg->numV; i++)
{
Data data;
while (LFirst(&(pg->adjList[i]), &data))
{
LRemove(&(pg->adjList[i]));
}
}
free(pg->adjList);
pg->numE = 0;
pg->numV = 0;
if (pg->visitInfo != NULL)
{
free(pg->visitInfo);
}
}
void AddEdge(ALGraph* pg, int fromV, int toV, int weight)
{
LInsert(&(pg->adjList[fromV]), toV);
LInsert(&(pg->adjList[toV]), fromV);
pg->numE++;
//추가된 부분, 간선의 정보를 힙에 저장
Edge edge = { fromV, toV, weight };
HInsert(&(pg->heap), edge);
}
void ShowGraphEdgeInfo(ALGraph* pg)
{
int i;
for (i = 0; i < pg->numV; i++)
{
printf("%c와 연결된 정점 : ", i + 'A');
Data data;
if (LFirst(&(pg->adjList[i]), &data))
{
printf("%c ", data + 'A');
while (LNext(&(pg->adjList[i]), &data))
{
printf("%c ", data + 'A');
}
}
else
{
printf("없음");
}
printf("\n");
}
}
int VisitVertex(ALGraph* pg, int visitV)
{
if (pg->visitInfo[visitV] == 0)
{
pg->visitInfo[visitV] = 1;
printf("%c ", visitV + 'A');
return TRUE;
}
return FALSE;
}
void BFShowGraphVertex(ALGraph* pg, int startV)
{
Queue queue;
int visitV = startV;
int nextV;
QueueInit(&queue);
VisitVertex(pg, visitV);
while (LFirst(&(pg->adjList[visitV]), &nextV))
{
if (VisitVertex(pg, nextV))
{
Inqueue(&queue, nextV);
}
while (LNext(&(pg->adjList[visitV]), &nextV))
{
if (VisitVertex(pg, nextV))
{
Inqueue(&queue, nextV);
}
}
if (QueueIsEmpty(&queue))
{
break;
}
else
{
visitV = Dequeue(&queue);
}
}
memset(pg->visitInfo, 0, sizeof(int) * pg->numV);
}
//추가된 함수, 방향성을 가지는 간선을 삭제하는 함수
//RemoveEdge 함수 안에서 호출됨
void RemoveWayEdge(ALGraph* pg, int fromV, int toV)
{
int vertex;
if (LFirst(&(pg->adjList[fromV]), &vertex))
{
if (vertex == toV)
{
LRemove(&(pg->adjList[fromV]));
return;
}
while (LNext(&(pg->adjList[fromV]), &vertex))
{
if (vertex == toV)
{
LRemove(&(pg->adjList[fromV]));
return;
}
}
}
}
//추가된 함수, 간선을 삭제하는 함수
//ConKruskalMST 함수 안에서 호출됨
void RemoveEdge(ALGraph* pg, int fromV, int toV)
{
RemoveWayEdge(pg, fromV, toV);
RemoveWayEdge(pg, toV, fromV);
pg->numE--;
}
//추가된 함수, 삭제했던 간선을 다시 복원하는 함수
//ConKruskalMST 함수 안에서 호출됨
void RecoverEdge(ALGraph* pg, int fromV, int toV, int weight)
{
LInsert(&(pg->adjList[fromV]), toV);
LInsert(&(pg->adjList[toV]), fromV);
pg->numE++;
}
//추가된 함수, 두 정점이 다른 간선에 의해 연결되어 있는지 확인하는 함수
//BFS 방법 활용
//ConKruskalMST 함수 안에서 호출됨
int IsConnVertex(ALGraph* pg, int fromV, int toV)
{
Queue queue;
int visitV = fromV;
int nextV;
QueueInit(&queue);
VisitVertex(pg, visitV);
while (LFirst(&(pg->adjList[visitV]), &nextV))
{
if (nextV == toV)
{
memset(pg->visitInfo, 0, sizeof(int) * pg->numV);
return TRUE;
}
if (VisitVertex(pg, nextV))
{
Inqueue(&queue, nextV);
}
while (LNext(&(pg->adjList[visitV]), &nextV))
{
if (nextV == toV)
{
memset(pg->visitInfo, 0, sizeof(int) * pg->numV);
return TRUE;
}
if (VisitVertex(pg, nextV))
{
Inqueue(&queue, nextV);
}
}
if (QueueIsEmpty(&queue))
{
break;
}
else
{
visitV = Dequeue(&queue);
}
}
memset(pg->visitInfo, 0, sizeof(int) * pg->numV);
return FALSE;
}
//추가된 함수, 최소 비용 신장 트리로 바꿈
void ConKruskalMST(ALGraph* pg)
{
Edge recvEdge[20]; //복원할 간선의 정보 저장
int edgeIndex = 0;
while (pg->numE + 1 > pg->numV) //간선의 수 + 1이 정점의 수와 같아질 때까지 반복
{
Edge edge = HDelete(&(pg->heap));
RemoveEdge(pg, edge.vertex1, edge.vertex2); //간선을 삭제
if (!IsConnVertex(pg, edge.vertex1, edge.vertex2)) //두 정점을 잇는 다른 간선이 존재하지 않는다면
{
RecoverEdge(pg, edge.vertex1, edge.vertex2, edge.weight); //삭제된 간선 다시 복원
recvEdge[edgeIndex++] = edge;
}
}
//힙에서 삭제된 간선의 정보를 회복
int i;
for (i = 0; i < edgeIndex; i++)
{
HInsert(&(pg->heap), recvEdge[i]);
}
}
//추가된 함수, 간선의 가중치 정보를 출력
void ShowGraphEdgeWeightInfo(ALGraph* pg)
{
Heap copyHeap = pg->heap;
Edge edge;
while (!HeapIsEmpty(©Heap))
{
edge = HDelete(©Heap);
printf("(%c, %c), weight : %d\n", edge.vertex1 + 'A', edge.vertex2 + 'A', edge.weight);
}
}위 파일에서 우선은 다음의 함수를 먼저 보겠습니다.
//추가된 함수, 최소 비용 신장 트리로 바꿈
void ConKruskalMST(ALGraph* pg)
{
Edge recvEdge[20]; //복원할 간선의 정보 저장
int edgeIndex = 0;
while (pg->numE + 1 > pg->numV) //간선의 수 + 1이 정점의 수와 같아질 때까지 반복
{
Edge edge = HDelete(&(pg->heap));
RemoveEdge(pg, edge.vertex1, edge.vertex2); //간선을 삭제
if (!IsConnVertex(pg, edge.vertex1, edge.vertex2)) //두 정점을 잇는 다른 간선이 존재하지 않는다면
{
RecoverEdge(pg, edge.vertex1, edge.vertex2, edge.weight); //삭제된 간선 다시 복원
recvEdge[edgeIndex++] = edge;
}
}
//힙에서 삭제된 간선의 정보를 회복
int i;
for (i = 0; i < edgeIndex; i++)
{
HInsert(&(pg->heap), recvEdge[i]);
}
}위 함수가 그래프를 최소 비용 신장 트리로 바꾸는 함수입니다. 그리고 위 함수 안에서 다음의 함수들이 호출됩니다.
//추가된 함수, 간선을 삭제하는 함수
//ConKruskalMST 함수 안에서 호출됨
void RemoveEdge(ALGraph* pg, int fromV, int toV)
{
RemoveWayEdge(pg, fromV, toV);
RemoveWayEdge(pg, toV, fromV);
pg->numE--;
}
//추가된 함수, 삭제했던 간선을 다시 복원하는 함수
//ConKruskalMST 함수 안에서 호출됨
void RecoverEdge(ALGraph* pg, int fromV, int toV, int weight)
{
LInsert(&(pg->adjList[fromV]), toV);
LInsert(&(pg->adjList[toV]), fromV);
pg->numE++;
}
//추가된 함수, 두 정점이 다른 간선에 의해 연결되어 있는지 확인하는 함수
//BFS 방법 활용
//ConKruskalMST 함수 안에서 호출됨
int IsConnVertex(ALGraph* pg, int fromV, int toV)
{
Queue queue;
int visitV = fromV;
int nextV;
QueueInit(&queue);
VisitVertex(pg, visitV);
while (LFirst(&(pg->adjList[visitV]), &nextV))
{
if (nextV == toV)
{
memset(pg->visitInfo, 0, sizeof(int) * pg->numV);
return TRUE;
}
if (VisitVertex(pg, nextV))
{
Inqueue(&queue, nextV);
}
while (LNext(&(pg->adjList[visitV]), &nextV))
{
if (nextV == toV)
{
memset(pg->visitInfo, 0, sizeof(int) * pg->numV);
return TRUE;
}
if (VisitVertex(pg, nextV))
{
Inqueue(&queue, nextV);
}
}
if (QueueIsEmpty(&queue))
{
break;
}
else
{
visitV = Dequeue(&queue);
}
}
memset(pg->visitInfo, 0, sizeof(int) * pg->numV);
return FALSE;
}코드가 어렵게 보이지만 하나하나 따라서 작성해보며 어떻게 동작하는지 생각해 보면 이해할 수 있습니다.
여기까지 해서 크루스칼 알고리즘의 구현이 완료됐습니다. 이제 나머지 파일들을 보이고, main 함수를 적절히 정의하여 그 실행결과를 확인해 보겠습니다.
//LLBQueue.h
//수정날짜 : 2021.03.28
//작성자 : KOEY
#ifndef LINKED_LIST_BASE_QUEUE_H
#define LINKED_LIST_BASE_QUEUE_H
#define TRUE 1
#define FALSE 0
typedef int QData;
typedef struct QNode
{
QData data;
struct QNode* next;
}QNode;
typedef struct LLBQueue
{
QNode* tail;
}LLBQueue;
typedef LLBQueue Queue;
void QueueInit(Queue* pq);
int QueueIsEmpty(Queue* pq);
void Inqueue(Queue* pq, QData data);
QData Dequeue(Queue* pq);
QData QPeek(Queue* pq);
void DeleteQueue(Queue* pq);
#endif//LLBQueue.c
//수정날짜 : 2021.03.28
//작성자 : KOEY
#include "LLBQueue.h"
#include <stdlib.h>
#include <stdio.h>
void QueueInit(Queue* pq)
{
pq->tail = NULL;
}
int QueueIsEmpty(Queue* pq)
{
if (pq->tail == NULL)
{
return TRUE;
}
return FALSE;
}
void Inqueue(Queue* pq, QData data)
{
QNode* newNode = (QNode*)malloc(sizeof(QNode));
if (newNode == NULL)
{
printf("메모리 공간이 부족합니다.\n");
exit(1);
}
newNode->data = data;
if (pq->tail == NULL)
{
newNode->next = newNode;
}
else
{
newNode->next = pq->tail->next;
pq->tail->next = newNode;
}
pq->tail = newNode;
}
QData Dequeue(Queue* pq)
{
QNode* delNode = pq->tail->next;
QData delData = delNode->data;
if (pq->tail == delNode)
{
pq->tail = NULL;
}
else
{
pq->tail->next = delNode->next;
}
free(delNode);
return delData;
}
QData QPeek(Queue* pq)
{
return pq->tail->next->data;
}
void DeleteQueue(Queue* pq)
{
while (!QueueIsEmpty(pq))
{
Dequeue(pq);
}
}
//LinkedList.h 헤더 파일로 저장
//수정 날짜 : 2021.03.25
//작성자 : KOEY
#ifndef LINKED_LIST_H
#define LINKED_LIST_H
#define TRUE 1
#define FALSE 0
typedef int Data;
typedef struct Node
{
Data data;
struct Node* next;
} Node;
typedef struct LinkedList
{
Node* head;
Node* cur;
Node* before;
int numOfData;
}LinkedList;
typedef LinkedList List;
void ListInit(List* plist);
void LInsert(List* plist, Data data);
int LFirst(List* plist, Data* pdata);
int LNext(List* plist, Data* pdata);
Data LRemove(List* plist);
int LCount(List* plist);
#endif//LinckedList.c 소스 파일로 저장
//수정 날짜 : 2021.03.25
//작성자 : KOEY
#include "LinkedList.h"
#include <stdlib.h>
#include <stdio.h>
void ListInit(List* plist)
{
plist->head = NULL;
plist->numOfData = 0;
}
void LInsert(List* plist, Data data)
{
Node* newNode = (Node*)malloc(sizeof(Node));
if (newNode == NULL)
{
printf("메모리 공간이 부족합니다.");
exit(1);
}
newNode->data = data;
if (plist->head == NULL)
{
newNode->next = NULL;
}
else
{
newNode->next = plist->head;
}
plist->head = newNode;
plist->numOfData++;
}
int LFirst(List* plist, Data* pdata)
{
plist->cur = plist->head;
plist->before = NULL;
if (plist->cur == NULL)
{
return FALSE;
}
*pdata = plist->cur->data;
return TRUE;
}
int LNext(List* plist, Data* pdata)
{
plist->before = plist->cur;
plist->cur = plist->cur->next;
if (plist->cur == NULL)
{
return FALSE;
}
*pdata = plist->cur->data;
return TRUE;
}
Data LRemove(List* plist)
{
Node* delNode = plist->cur;
Data delData = delNode->data;
plist->cur = plist->before;
if (delNode == plist->head)
{
plist->head = delNode->next;
}
else
{
plist->before->next = delNode->next;
}
free(delNode);
plist->numOfData--;
return delData;
}
int LCount(List* plist)
{
return plist->numOfData;
}
//main.c
//수정날짜 : 2021.03.27
//작성자 : KOEY
#include <stdio.h>
#include "ALGraphKruskal.h"
int main(void)
{
ALGraph graph; //그래프의 생성
GraphInit(&graph, 6); //그래프의 초기화
AddEdge(&graph, A, B, 9);
AddEdge(&graph, B, C, 2);
AddEdge(&graph, A, C, 12);
AddEdge(&graph, A, D, 8);
AddEdge(&graph, D, C, 6);
AddEdge(&graph, A, F, 11);
AddEdge(&graph, F, D, 4);
AddEdge(&graph, D, E, 3);
AddEdge(&graph, E, C, 7);
AddEdge(&graph, F, E, 13);
ShowGraphEdgeInfo(&graph); //그래프의 간선 정보 출력
ConKruskalMST(&graph); //MST로 변환
printf("\n");
ShowGraphEdgeInfo(&graph); //그래프의 간선 정보 출력
ShowGraphEdgeWeightInfo(&graph);
GraphDestroy(&graph); //그래프의 리소스 소멸
return 0;
}
/*
실행결과
A와 연결된 정점 : F D C B
B와 연결된 정점 : C A
C와 연결된 정점 : E D A B
D와 연결된 정점 : E F C A
E와 연결된 정점 : F C D
F와 연결된 정점 : E D A
F D A A F D B E A D B E A D E F C A E D A F
A와 연결된 정점 : D
B와 연결된 정점 : C
C와 연결된 정점 : D B
D와 연결된 정점 : A E F C
E와 연결된 정점 : D
F와 연결된 정점 : D
(A, D), weight : 8
(D, C), weight : 6
(F, D), weight : 4
(D, E), weight : 3
(B, C), weight : 2
*/'공부 일지 > 자료구조 공부 일지' 카테고리의 다른 글
| Chapter 14. 그래프의 탐색 (3) (0) | 2021.03.29 |
|---|---|
| Chapter 14. 그래프의 탐색 (2) (0) | 2021.03.29 |
| 연습문제 14. 01 DFS의 탐색 과정 (0) | 2021.03.27 |
| Chapter 14. 그래프의 탐색 (0) | 2021.03.27 |
| Chapter 14. 인접 리스트 기반의 그래프 구현 (0) | 2021.03.27 |
