티스토리 뷰
주의 사항!
- 이 글은 제가 직접 공부하는 중에 작성되고 있습니다.
- 따라서 제가 이해하는 그대로의 내용이 포함됩니다.
- 따라서 이 글은 사실과는 다른 내용이 포함될 수 있습니다.
그저 잘 동작하는 자료구조와 알고리즘을 찾는 것이 목적이라면 기능별로 자료구조와 알고리즘을 하나씩만 알아도 됩니다. 하지만 우리는 잘 동작하는 것은 물론이거니와 좋은 성능까지 보장받기를 원합니다. 때문에 우리는 자료구조와 알고리즘을 분석하고 평가할 수 있어야 합니다. 모든 경우에 있어서 항상 우월한 성능을 보이는, 만능 키와 같은 자료구조와 알고리즘은 존재하지 않기 때문입니다.
자료구조와 알고리즘을 평가하는 두 가지 요소를 다음과 같이 정리할 수 있습니다.
- 어떤 자료구조와 알고리즘이 어떠한 상황에서 더 빠르고 또 느린가?
- 어떤 자료구조와 알고리즘이 어떠한 상황에서 메모리를 적게 쓰고 또 많이 쓰는가?
이렇듯 하나는 '속도'에 관한 것이고, 다른 하나는 '메모리의 사용량'에 관한 것인데, 속도에 해당하는 알고리즘의 수행시간 분석결과를 가리켜 '시간 복잡도'라 하고, 메모리 사용양에 대한 분석결과를 가리켜 '공간 복잡도'라고 합니다.
사실 메모리를 적게 쓰고 속도도 빨라야 최적의 알고리즘이라고 할 수 있습니다. 그런데 일반적으로 알고리즘을 평가할 때는 메모리의 사용량보다 실행속도에 초점을 둡니다. 물론 특정 알고리즘에 대해서 상대적인 우월성을 입증해야 하는 경우에는 메모리의 사용량도 함께 고려가 되지만, 이미 검증이 끝난 알고리즘의 적용을 고려하는 경우에는 속도에 초점을 두어 적합성 여부를 판단하게 됩니다.
그럼 속도를 어떻게 평가할 수 있을까요? 알고리즘의 속도를 평가하기 위해 수행시간을 측정할 수는 없습니다. 처리하는 데이터의 양의 변화에 따른 속도의 증감의 정도를 알아야 하는데, 이를 위해서 조건을 달리하여 수백 번, 수천 번 실행해가면서 시간을 잴 수는 없는 일이기 때문입니다.
그래서 알고리즘의 수행속도를 평가할 때는 다음과 같은 방식을 취합니다.
- 연산의 횟수를 셉니다.
- 그리고 처리해야할 데이터의 수 n에 대한 연산횟수의 함수 T(n)을 구성합니다.
말 그대로 연산의 횟수를 통해서 알고리즘의 빠르기를 판단합니다. 물론 연산의 횟수가 적어야 빠른 알고리즘입니다. 그리고 데이터의 수 n에 대한 연산횟수의 함수 T(n)을 구성하는 이유는, 식을 구성하면 데이터의 수의 증가에 따른 연산횟수의 변화 정도를 판단할 수 있기 때문입니다.
즉, 알고리즘 별 연산횟수를 함수 T(n)의 형태로 구성하면, 다음 그림에서 보이는 바와 같이 그래프를 통해서 데이터 수의 변화에 따른 연산횟수의 변화 정도를 한 눈에 파악할 수 있으며, 이로 인해서 둘 이상의 알고리즘을 비교하기가 용이해 집니다.

위 그림에서 보이는 것이 동일한 기능을 제공하는 서로 다른 두 알고리즘의 성능을 비교한 결과라고 가정해 보겠습니다. 두 알고리즘을 비교해보면, 데이터의 수가 적은 경우 알고리즘 B의 속도가 빠르지만 데이터의 수가 많아지면 알고리즘 A의 속도가 더 빠르다는 것을 확인할 수 있습니다. 그러면 위의 분석결과를 토대로 다음과 같이 판단할 수 있습니다.
- 데이터의 수가 적은 경우에는 알고리즘B를 적용하고, 데이터의 수가 많은 경우에는 알고리즘A를 적용해야지
나름 합리적인 판단이고 실제로 이렇게 판단하고 적용하기도 합니다. 하지만 데이터의 수가 적은 경우, 속도 차이가 나봐야 얼마나 날까요? 중요한 것은 데이터의 수가 많아짐에 따른 연산횟수의 증가 정도에 있습니다. 따라서 알고리즘 A가 훨씬 좋은 알고리즘이라고 할 수 있습니다.
하지만 그렇다고 알고리즘 B를 무시할 수는 없습니다. 대게 A와 같이 안정적인 성능을 보장하는 알고리즘은 B와 같은 성격의 알고리즘에 비해서 구현의 난이도가 높은 편입니다. 따라서 어차피 다룰 데이터의 수가 많지 않거나, 성능에 덜 민감한 경우라면 구현의 편의를 이유로 B와 같은 알고리즘을 선택하기도 합니다.
이 책의 저자는 알고리즘을 선택함에 있어 상황에 맞게 답을 내려야 한다고 말합니다. 따라서 이 책의 저자는 우리들이 알고리즘의 구현능력에만 관심을 두는 것을 바라지 않습니다. 어찌 보면 구현보다 중요한 것은 종합적으로 사고하고 판단하는 능력이기 때문입니다.
이번에는 '순차 탐색 알고리즘'이라는 매우 간단한 탐색 알고리즘 하나를 소개하고 이를 대상으로 시간 복잡도를 계산해 보겠습니다. 먼저 순차 탐색 알고리즘을 적용한 예제입니다.
#include <stdio.h>
int LSearch(int arr[], int len, int target) //순차 탐색 알고리즘 적용된 함수
{
int i;
for (i = 0; i < len; i++)
{
if (arr[i] == target) return i; //찾은 대상의 인덱스 값 반환
}
return -1; //찾지 못했음을 의미하는 값 반환
}
int main(void)
{
int arr[] = { 3, 5, 2, 4, 9 };
int index = LSearch(arr, sizeof(arr) / sizeof(arr[0]), 4);
if (index == -1) printf("탐색 실패!");
else printf("타겟 저장 인덱스 : %d\n", index);
index = LSearch(arr, sizeof(arr) / sizeof(arr[0]), 7);
if (index == -1) printf("탐색 실패!");
else printf("타겟 저장 인덱스 : %d\n", index);
return 0;
}
/*
실행결과
타겟 저장 인덱스 : 3
탐색 실패!
*/위 예제의 LSearch 함수에서 보이는 것은 순차 탐색 알고리즘입니다. 맨 앞에서부터 순서대로 탐색을 진행하는 알고리즘이기 때문에 순차 탐색이라는 이름이 붙었습니다. 순차 탐색 알고리즘을 실제로 구현하는 코드만 별도로 떼어 놓고 보겠습니다.
for (i = 0; i < len; i++)
{
if (arr[i] == target) return i; //찾은 대상의 인덱스 값 반환
}이제 위의 코드를 토대로 시간 복잡도를 분석해서 데이터의 수 n에 대한 연산횟수의 함수 T(n)을 구해 봅니다.
위 코드에서 사용된 연산은 <, ++, ==입니다. 그럼 이 세 개의 연산횟수를 모두 세어야 할 것 같습니다. 하지만 잘 생각해보면 우리가 따져야할 연산은 == 하나입니다. 순차 탐색 알고리즘의 핵심은 배열 요소의 값이 찾고자 하는 값과 동일한가? 입니다. 즉, 어느 배열 요소의 값과 target 값이 동등한지를 비교하는 == 비교 연산자가 이 알고리즘의 핵심 연산이 됩니다. 나머지 <와 ++은 ==연산에 종속적이게 됩니다. ==연산이 비교적 덜 수행되면 <나 ++도 그만큼 적게 수행될 것이고, ==연산이 비교적 많이 수행되면 <나 ++도 그만큼 많이 수행될 것입니다.
(저는 사실 위 의견에 꼭 동의하지는 못합니다. 저는 데이터의 개수 n에 대한 연산횟수 T(n) 함수를 만들 때 고려해야 할 연산이란, CPU가 메모리에 접근하는 횟수를 의미한다고 생각했습니다.
CPU는 연산장치이지 데이터 저장 장치는 아닙니다. 즉 CPU자체는 데이터를 받아서 어느 연산 과정에 따라 처리할 뿐, 데이터 그 자체를 어딘가에 저장할 공간은 없습니다. 그래서 CPU가 어느 연산을 한 번 하기 위해서는 연산에 사용될 변수들을 메모리에게서 가져와야 합니다. 데이터 개수에 따른 연산횟수를 비교하는 이유는 알고리즘의 속도를 비교하기 위함입니다. 따라서 똑같은 일을 처리하더라도 무엇이 더 빠르고 효율적인 작업방식인가를 가려내기 위함입니다.
프로그램 실행 중에 속도를 더디게 할 만한 요소는 CPU와 메모리 간의 통신 시간이 주로 작용한다고 생각합니다. 즉, CPU가 연산에 사용할 데이터를 메모리로부터 가져올 때 걸리는 시간, 혹은 연산 결과를 메모리에 저장할 때 걸리는 시간들이 프로그램의 성능에, 알고리즘의 성능에 영향을 미친다고 생각합니다.
그런 관점에서 보면 CPU가 메모리와 접촉해야 할 일을 최대한 적게 만들어 주는 것이 효율적인 알고리즘이라고 생각합니다. 따라서 변수를 선언하고 저장하는 것, 비교 연산 뿐만 아니라 <연산과 ++연산까지, 더 세세하게 따져서는 배열요소에 접근해서 값을 가져오는 것 하나, target 변수에 접근해서 값을 가져오는 것 둘, 두 개의 값을 비교하는 것 셋까지 세세히 연산횟수에 포함해야 한다고 생각합니다.)
이제 순차 탐색 알고리즘의 비교연산횟수를 계산해 보겠습니다. 순차 탐색 알고리즘에서는 운이 좋아서 찾고자 하는 값이 배열의 맨 앞에 있을 수도 있지만, 운이 나쁘면 배열의 마지막에 있을 수 있습니다. 즉 운이 좋으면 연산횟수는 1, 운이 나쁘면 연산횟수는 n(배열 요소의 개수)이 되는 것입니다. 이를 전문용어로 '최선의 경우'와 '최악의 경우'라고 합니다.
그런데 알고리즘을 평가하는 데 있어서 '최선의 경우'는 관심 대상이 아닙니다. 어떠한 알고리즘이건 최선의 경우는 대부분 만족할 만한 결과를 보이기 때문입니다. 따라서 알고리즘의 성능을 판단하는 데 있어서 중요한 것은 '최악의 경우'입니다.
여기서 최선도 최악도 아닌 평균적인 경우를 따지는 것이 더 좋다고 생각할지도 모릅니다. 물론 평균적인 경우를 비교할 수 있다면 좋은 방법입니다. 하지만 그런 평균을 내는 것이 쉽지 않습니다. 이를 계산하기 위해서는 다양한 이론이 적용되어야 하고, 분석에 필요한 여러 가지 시나리오와 데이터를 현실적이고 합리적으로 구성해야 하는데 이는 쉽지 않은 일입니다.
결국 일반적인 알고리즘의 평가에는 논란의 소지가 거의 없는 '최악의 경우'가 선택될 수 밖에 없습니다.
위에서 보인 순차 탐색 알고리즘의 최악의 경우에 시간 복잡도는 T(n) = n 입니다.
이번에는 앞서 설명한 순차 탐색 알고리즘보다 훨씬 좋은 성능을 보이는 이진 탐색 알고리즘을 소개하겠습니다. 배열을 대상으로 이진 탐색 알고리즘을 적용하기 위해서는 배열에 저장된 데이터가 정렬되어 있어야 합니다. 즉, 이진 탐색 알고리즘은 정렬된 데이터가 아니면 적용이 불가능합니다.
다음과 같은 배열에 데이터가 정렬되어 있다고 가정하겠습니다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 7 | 9 | 12 | 21 | 23 | 27 | 32 |
위 배열에서 숫자 21을 찾으려고 합니다. 이진 탐색 알고리즘은 다음과 같은 과정을 거쳐 숫자 21을 찾습니다.
먼저, 배열의 수가 0번 부터 9번까지 총 10개입니다. 가장 첫 번호인 0과 가장 마지막 번호인 9를 더하고 이 결과값을 2로 나눕니다. 이때 나머지는 버립니다. 그러면 결과는 4가 됩니다.
이제 위 배열의 4번 요소에 접근해서 해당 데이터가 21이 맞는지 확인합니다. 만약 아니라면 4번 요소의 데이터와 21 중 무엇이 더 큰지 비교합니다. 4번 요소에는 9가 저장되어 있으므로 21이 더 큽니다. 따라서 숫자 21은 4번 요소보다는 뒤에 있을 것이라 생각하고 0번부터 4번까지의 값은 무시합니다.
이제 이 알고리즘이 탐색할 범위가 다음과 같이 줄었습니다.
| 5 | 6 | 7 | 8 | 9 |
| 12 | 21 | 23 | 27 | 32 |
다시 위 과정을 반복합니다. 가장 첫 번째 번호인 5와 마지막 번호인 9를 더하고 이를 2로 나눕니다. 결과 값은 7이 됩니다.
이제 위 배열의 7번 요소에 접근해서 해당 데이터가 21이 맞는지 확인합니다. 만약 아니라면 해당 값과 21 중에 무엇이 더 큰지 비교합니다. 이번에는 7번 요소의 값 23보다 21이 작습니다. 그러면 알고리즘은 7번 요소 보다는 앞에 21이 있을 것이라고 생각하고 7번 이상의 요소들은 무시합니다.
이제 이 알고리즘이 탐색할 범위가 다음과 같이 줄었습니다.
| 5 | 6 |
| 12 | 21 |
같은 방식으로 이제 5번 요소에 접근했다가, 결국에는 마지막 남은 6번 요소의 값을 찾게 될 것입니다.
이제 앞서 설명한 이진 탐색 알고리즘을 코드로 구현해 보겠습니다. 다음 예제에서 정의하고 있는 BSearch 함수가 이진 탐색 알고리즘의 구현에 해당합니다.
//main.c 소스 파일로 저장
#include <stdio.h>
int BSearch(int arr[], int len, int target) //이진 탐색 알고리즘 적용된 함수
{
int first = 0, last = len - 1;
while (first <= last)
{
int mid = (first + last) / 2;
if (arr[mid] == target) return mid;
else
{
if (arr[mid] < target) first = mid + 1;
else last = mid - 1;
}
}
return -1;
}
int main(void)
{
int arr[] = { 1, 2, 3, 7, 9, 12, 21, 23, 27, 32 };
int index = BSearch(arr, sizeof(arr) / sizeof(arr[0]), 21);
if (index == -1) printf("탐색 실패!");
else printf("타겟 저장 인덱스 : %d\n", index);
index = BSearch(arr, sizeof(arr) / sizeof(arr[0]), 4);
if (index == -1) printf("탐색 실패!");
else printf("타겟 저장 인덱스 : %d\n", index);
return 0;
}
/*
타겟 저장 인덱스 : 6
탐색 실패!
*/이제 최악의 경우를 기준으로 이진 탐색 알고리즘의 시간 복잡도를 계산해 보겠습니다. 먼저 다음의 이진 탐색 알고리즘을 보면서 연산횟수를 대표하는 연산이 무엇인지 찾아봅니다.
while (first <= last)
{
int mid = (first + last) / 2;
if (arr[mid] == target) return mid;
else
{
if (arr[mid] < target) first = mid + 1;
else last = mid - 1;
}
}이 경우에도 핵심 연산은 ==대입 연산입니다. 맞는 값을 찾을 때까지 다른 과정들을 반복할 것이기 때문입니다.
계산하기 전에 말하자면 모든 경우에 있어서(모든 데이터 개수에 있어서) 딱 정확하게 맞아 떨어지는 값(데이터 수에 따른 연산 횟수)을 계산하기는 힘듭니다. 그래서 근사치의 개념으로 함수 T(n)를 구하게 될 것입니다.
해당 연산이 이뤄지는 알고리즘을 간단하게 생각해 보겠습니다. 이진 탐색 알고리즘은 처음 주어진 범위를 절반씩 날려가면서 탐색 범위를 좁혀 나갑니다. 얼마 좁히지 않아도 운이 좋게 찾는 값을 찾을 수도 있지만, 운이 나쁘다면 범위를 줄이다 줄이다 결국 하나만 남을 때까지 연산을 계속하게 될 것입니다. 그리고 하나가 남아도 그 하나의 값이 맞는 값인지 확인하는 연산을 또 수행합니다.
따라서 이진 탐색 알고리즘에 있어서 최악의 경우는 범위를 좁히다 좁히다 마지막 하나가 남을 때까지 값을 찾지 못하는 경우가 될 것입니다. 그렇게 최악의 경우를 정의하고나서 생각하면 이진 탐색 알고리즘의 T(n) 함수를 왜 근사치로 밖에 구할 수 없는지 알 수 있습니다.
주어진 데이터가 4개라고 가정해 보겠습니다. 0번 부터 3번까지 있으므로 먼저 1번의 데이터를 확인하게 될 것입니다. 이로써 연산이 한 번 수행됩니다. 만약 1번 값이 맞지 않는다면 범위를 새로 좁혀야 합니다. 그런데 어느 쪽으로 범위를 좁힐 것이냐에 따라서 연산횟수가 달라집니다.
만약 1보다 낮은 쪽으로 범위를 좁힌다고 가정해보겠습니다. 그렇게 되면 남은 데이터는 0번 하나입니다. 따라서 0번에 대한 데이터 비교 연산을 수행하고, 총 연산횟수는 2회가 됩니다. 반대로 1보다 높은 쪽으로 범위를 좁힌다고 가정해보겠습니다. 그렇게 되면 2번과 3번이 남습니다. 이에 알고리즘은 2번에 대한 비교연산을 수행하고, 맞지 않으면 3번에 대한 비교 연산을 수행합니다. 따라서 총 연산횟수는 3회가 됩니다.
위에서 든 예는 똑같은 데이터의 수에 대해 똑같이 정의된 최악의 경우에 대해 연산횟수를 비교해 봐도 그 값이 2회와 3회로 달라짐을 확인시켜 주었습니다. 이것이 이진 탐색 알고리즘을 근사치로 구해야 하는 이유가 됩니다.
이진 탐색 알고리즘의 시간 복잡도를 근사치로 구하기 위해 생각해 볼 것이 있습니다. 처음 주어지는 데이터의 개수가 s개 라면, 처음 이 s에 대해 탐색을 한 번 수행합니다. 그러고 찾지 못하면 데이터의 개수는 2로 나뉘어져 s/2가 됩니다. 이 범위에서도 찾지 못하면 다시 2로 나누어 데이터의 개수는 s/4가 됩니다. 즉 데이터의 개수는 연산횟수에 대해 다음과 같이 됩니다.
| 연산횟수 | 1 | 2 | 3 | 4 | ... | n |
| 데이터 개수 | s | s/2 | s/4 | s/8 | ... | s/2^(n-1) |
만약 데이터 개수를 줄이다 줄이다 1이하가 되면 값을 찾게 될 것입니다. 따라서 s/2^(n-1)이 1이하가 되도록 하는 가장 작은 정수 n값이 이진 탐색 알고리즘의 시간 복잡도가 됩니다.
여기서는 수식의 모양이 이쁘게 나오지 않아서 PPT에서 수식을 만들어 캡쳐하여 올리겠습니다.
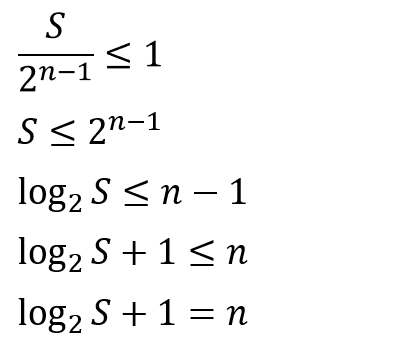
데이터 개수 S에 대한 연산횟수 n은 위 식과 같습니다. 부등호에서 갑자기 등호로 바뀌게 된 이유는 다음과 같습니다.
위 범위의 모든 n값이 연산횟수가 되는 것이 아니라 위 범위를 만족하는 n값 중에서 가장 작은 값이 최악의 경우 연산횟수에 해당되는데, 이런 자잘한 조건까지 구현할 수는 없고, 어차피 해당 관계도 근사치로서 유도한 것이기 때문에 위 수식을 만족하는 n값을 최악의 경우 연산횟수로 한다는 결정(?)이 들어간 것입니다.
해당 함수를 그래프로 표현하면 다음과 같습니다.
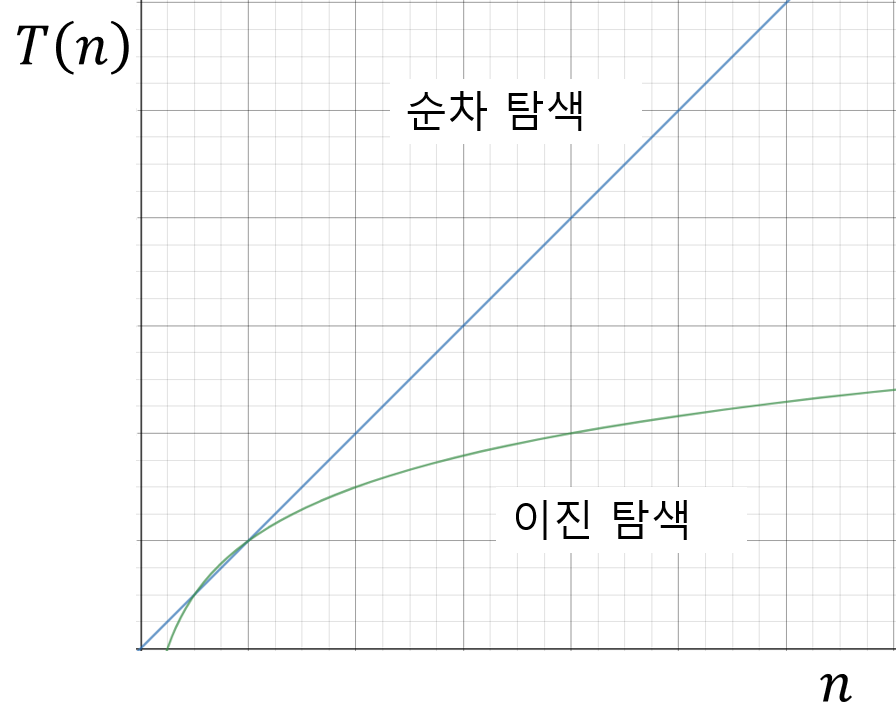
순차 탐색과 비교했을 때 데이터의 개수가 많아져도 연산횟수가 크게 증가하지 않는 모양새로 보았을 때 이진 탐색 알고리즘이 순차탐색 알고리즘보다 훨씬 효율적이고 빠르다는 것을 알 수 있습니다.
'공부 일지 > 자료구조 공부 일지' 카테고리의 다른 글
| Chapter 02. 함수의 재귀적 호출의 이해 (0) | 2021.03.07 |
|---|---|
| Chapter 01. 빅-오에 대한 수학적 접근 (0) | 2021.03.07 |
| Chapter 01. 알고리즘의 성능 분석 방법 2 (0) | 2021.03.07 |
| Chapter 01. 자료구조(Data Structure)에 대한 기본적인 이해 (0) | 2021.03.06 |
| 자료구조 공부에 앞서... (0) | 2021.03.06 |
