티스토리 뷰
주의 사항!
- 이 글은 제가 직접 공부하는 중에 작성되고 있습니다.
- 따라서 제가 이해하는 그대로의 내용이 포함됩니다.
- 따라서 이 글은 사실과는 다른 내용이 포함될 수 있습니다.
이전 시간에 이진 탐색 알고리즘의 시간복잡도를 구했습니다. 이진 탐색 알고리즘의 T(n)은 다음과 같았습니다.

그런데 계산하기에 따라서는 똑같은 이진 탐색 알고리즘에 대해 시간 복잡도가 다음과 같이 구해질 수도 있습니다.

그럼 여기에서 1을 더하는 것이 맞냐, 더하지 않는 것이 맞냐를 따지게 됩니다. 하지만 +1쯤이야 큰 의미가 없습니다. 물론 이는 1이 아니라 10000이었어도 큰 의미가 없다고 말할 수 있습니다. 그럼 여기서 이렇게 생각할지도 모릅니다.
'아니, 1쯤이야 뭐 우리도 무시할 수는 있겠다 생각하는데, 그래도 10000은 작은 수도 아닌데 무시해도 되는거냐'
이 물음에 대한 답은 '빅-오 표기법'에서 얻을 수 있습니다.
사실 데이터의 수 n과 그에 따른 시간 복잡도 함수 T(n)을 정확히 그리고 오차 없이 구하는 것은 대부분의 경우 불가능에 가깝습니다. 따라서 오차를 허용하지 않겠다면, 앞서 우리가 '+1을 넣는 게 맞네 틀리네' 하면서 옥신각신하겠지만, 오차를 허용한다면 함수를 어떤 관점에서 봐야 하는지, 즉, 어디까지 '오차'로 너그럽게 봐줄 수 있는지를 생각하게 됩니다.
빅-오 표기법에서는 함수에 가장 큰 영향을 미치는 인자만 따지라고 합니다. 예를 들어서 다음과 같은 함수가 있다고 가정할 때,

위 함수에서 가장 큰 영향력을 가지는 인자는 n^2입니다. 즉, 나머지 n+1은 오차로 너그럽게 봐줄 수 있다는 뜻이 됩니다. 어떻게 그런게 가능할까요? 먼저 위 함수의 그래프를 보겠습니다.

위 함수의 모양을 기억하기 바랍니다. 그리고 위 함수의 각 인자, n^2, n, 1의 그래프가 어떤 식으로 그려지는지 아래에 소개하겠습니다.



위의 그래프는 각각 n^2, n, 1에 대한 그래프를 나타낸 것입니다. 이들 그래프와 n^2+n+1의 그래프를 비교해 보면 가장 모양이 비슷한 인자는 n^2뿐임을 확인할 수 있습니다. 함수에 가장 영향력이 큰 인자란 바로 이렇듯, 함수의 모양에 가장 큰 영향력을 행사하는 인자를 말합니다. 그리고 함수의 모양에 가장 큰 영향력을 행사하는 인자만 따지는 빅-오 표기법은 함수 그래프를 보는 다음의 관점에서 의미를 가집니다.
다시 함수 n^2+n+1의 그래프를 보겠습니다. 해당 그래프를 보면서 가장 먼저 확인하는 것은 그래프의 위치가 아닙니다. 즉, 'n이 1일 때 함수값은 3이구나'를 보는 것이 아니라 'n이 증가할수록 함수값이 급격하게 증가하는구나'를 보게 됩니다. 그런 관점에서 봤을 때 똑같이 'n이 증가할수록 함수값이 급격하게 증가하는구나'같은 이미지를 주는 인자는 n^2입니다. 즉, 그래프를 보는 사람의 주요 관심사는 'n의 변화에 따라서 값이 어떤 모양새로 변하는가'이고, 해당 정보는 n^2인자 하나만으로도 전달이 가능하기 때문에 빅-오 표기법은 의미를 가집니다.
정리하면, T(n)=n^2+n+1은 T(n)=n^2으로 간략화할 수 있고, 이를 '빅-오 표기법'으로 표기하면 다음과 같습니다.

이는 '빅-오 오브 n제곱'으로 읽습니다. 그리고 위의 예에서 함수에 가장 큰 영향력을 행사하는 n^2와 같은 인자를 '빅-오'라고 부릅니다.
이쯤해서 어떠한 수식을 보고서 그 수식의 빅-오를 구하려면 매번 그래프를 그려서 모양새를 비교해봐야 하는 것인지 궁금할 수 있습니다. 하지만 그럴 필요는 없습니다. 수식을 보고서 빅-오를 구하는 간단한 방법이 있습니다. 바로 차수가 가장 높은 인자를 선택하는 것입니다.
예를 들어보겠습니다.

위와 같은 수식에서 각각 빅-오를 찾아봅니다. 첫 번째 수식부터 순서대로 빅-오는 n^2, n^3, n^5가 됩니다. 이들이 각각의 수식에서 가장 차수가 높습니다.
그런데 차수가 높은 인자를 선택하는 건 알겠는데 왜 2n^2, 3n^3, 10n^5가 아닌지 궁금할 수 있습니다. 사실 이건 저도 궁금합니다. 책에서도 그럴듯한 설명은 해주지 않는 것 같습니다. 다만, 스스로 이해하기에는 모양새 뿐만 아니라 함수의 주요한 특징을 반영하는 인자만 고려하는 것 같습니다.
무슨 말이냐 예를 들어 어느 수식이 다음과 같이 있다고 가정해 보겠습니다.

그렇다면, 위 수식의 빅-오는 17일까요? 1일까요? 위 수식은 다음과 같이 쓰일 수 있습니다.

이제는 빅-오를 찾기가 아까보다는 수월해졌을 것입니다. 그럼 빅-오는 17일까요? 1일까요? 빅-오를 17로 하면, 함수의 모양새와 빅-오의 모양새가 같게 됩니다. 반면, 1은 일직선인 모습은 같아도 위치가 달라서 17을 빅-오로 하는 것이 더 합리적으로 보이긴 합니다. 하지만 17이나 1이나 데이터의 개수 n의 변화에 상관없이 일정한 값을 보인다는 주요한 특징은 같습니다.
시간 복잡도를 계산하는 사람은 데이터의 변화량에 대해 연산횟수가 어떻게 변화하는지를 알고 싶을 뿐이기 때문에 굳이 17을 빅-오로 잡는 것은 투머치한 정보가 됩니다. 그래서 함수의 모양새, 주요한 특징을 명확히 알 수 있고 간결한 인자를 빅-오로 잡습니다.
마찬가지의 이유로

위 수식의 빅-오를 4n이 아닌 n으로 잡습니다. n만으로도 그래프가 직선형이고, 데이터 수의 증가에 비례해 똑같은 기울기로 연산횟수가 증가한다는 주요한 특징까지 알 수 있기 때문입니다.
대표적인 빅-오를 설명하겠습니다.

이를 상수형 빅-오라고 합니다. 이는 데이터 수에 상관없이 연산횟수가 고정인 유형의 알고리즘을 뜻합니다. 예를 들어서 연산의 횟수가 데이터 수에 상관없이 3회 진행되는 알고리즘일지라도 O(3)라고 하지 않고 O(I)라고 합니다.

이를 로그형 빅-오라고 합니다. 이는 '데이터 수의 증가율'에 비해서 '연산횟수의 증가율'이 훨씬 낮은 알고리즘을 의미합니다. 그래프를 통해 확인해 보겠습니다.
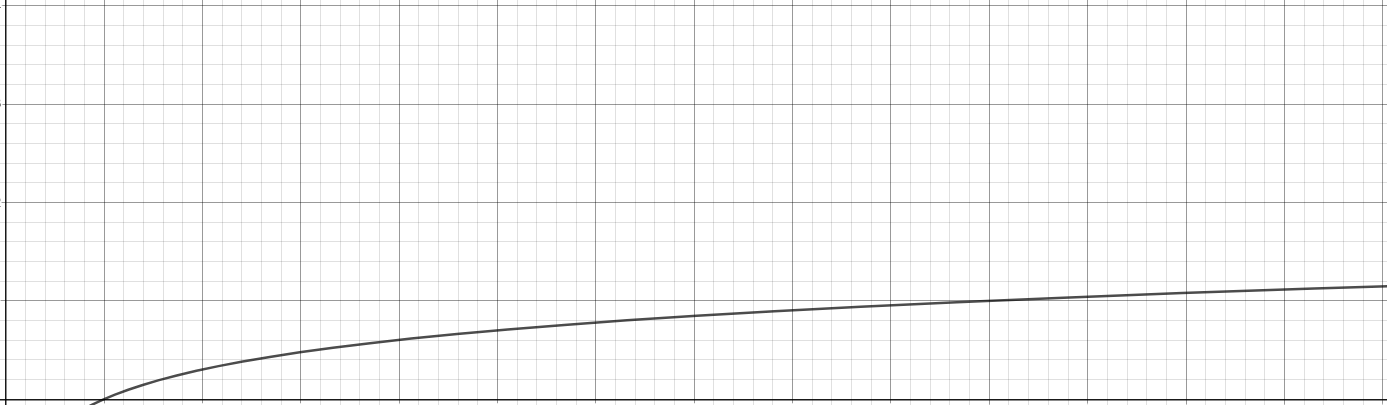
그래프를 보다시피 데이터의 수가 아무리 많아져도 연산횟수의 증가폭은 적습니다. 따라서 이런 유형의 알고리즘이 좋은 알고리즘이라고 할 수 있습니다. 참고로 로그의 밑이 얼마냐에 따라서 차이가 나긴 하지만 그 차이는 알고리즘의 성능관점에서 매우 미미하기 때문에 대부분의 경우에 있어서 무시가 됩니다.

이를 선형 빅-오라고 합니다. 이는 데이터의 수과 연산횟수가 비례하는 알고리즘을 의미합니다.

이를 선형로그형 빅-오라고 합니다.이는 데이터의 수가 두 배로 늘 때, 연산횟수는 두 배를 조금 넘게 증가하는 알고리즘을 의미합니다. 그래프를 통해 확인해 보겠습니다.

n과 logn을 곱한 형태라 난해해 보이지만, 알고리즘 중에는 이에 해당하는 알고리즘이 적지 않습니다.

이는 데이터 수의 제곱에 해당하는 연산횟수를 요구하는 알고리즘을 의미합니다. 따라서 데이터의 양이 많은 경우에는 적용하기가 부적절한데, 이는 이중으로 중첩된 반복문 내에서 알고리즘에 관련된 연산이 진행되는 경우에 발생합니다. 달리 말하면 중첩된 반복문의 사용은 알고리즘 디자인에서 그리 바람직하지 못하다고 할 수 있습니다.

데이터 수의 세제곱에 해당하는 연산횟수를 요구하는 알고리즘을 의미합니다. 이는 삼중으로 중첩된 반복문 내에서 알고리즘에 관련된 연산이 진행되는 경우에 발생합니다. 이 역시 그냥 적용하기에는 무리가 있는 알고리즘입니다.

이를 지수형 빅-오라고 합니다. 이는 사용하기에 매우 무리가 있는, 사용한다는 것 자체가 비현실적인 알고리즘입니다. '지수적 증가'라는 어마무시한 연산횟수의 증가를 보이기 때문입니다. 그래프로 확인해보면 다음과 같습니다.

'공부 일지 > 자료구조 공부 일지' 카테고리의 다른 글
| Chapter 02. 함수의 재귀적 호출의 이해 (0) | 2021.03.07 |
|---|---|
| Chapter 01. 빅-오에 대한 수학적 접근 (0) | 2021.03.07 |
| Chapter 01. 알고리즘의 성능 분석 방법 1 (0) | 2021.03.06 |
| Chapter 01. 자료구조(Data Structure)에 대한 기본적인 이해 (0) | 2021.03.06 |
| 자료구조 공부에 앞서... (0) | 2021.03.06 |
